The Math of Viral
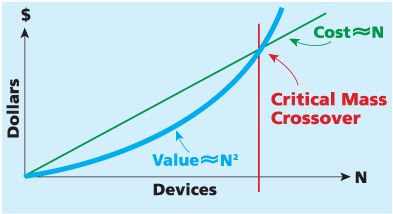
I've been working on this thing in my head for a while and it's still hardly played out. But I've got a thesis going that you can apply Metcalfe's Law to marketing. For those not familiar with it, Metcalfe's Law is a way to calculate the value of a network. In a recent Forbe's article Metcalfe himself explained it like this: "The network effect says that the value of that Ethernet card to the person on whose desk it sits is proportional to the number, N, of other computer users he can connect to. Now multiply this value by the number of users, and you have a value for the whole operation that is roughly proportional to N2." In plain English: If one person has a fax machine it's got no value, if two people have it, it's still got very little value. From there, however, the value really starts to grow for everyone involved and eventually it hits a 'tipping point' where you can't not have one.
[Taken from Metcalfe in Forbes]
As I've mentioned, power laws are a core part of our interconnected world and Metcalfe's Law speaks to how these things happen. Essentially, because there's more value to a network as it grows, eventually they reach a 'tipping point' (or 'critical mass crossover') where some serious growth kicks in (think about when everyone started texting you and you had no choice but to text back).
[WARNING: I am probably about to butcher some math. I apologize for that.]
Anyway, when I was looking at that graph of Metcalfe's Law, I realized that it's exactly what 'viral marketing' is attempting (as much as I hate that term). Essentially 'viral' (and PR) is an attempt to get value that goes above and beyond cost. In the old days of media buying you bought the number of impressions you wanted. It was a fairly straightforward equation: Value = cost, and cost is based on number of impressions (N) times CPM (cost per thousand impressions). 'Viral' tries to beat the system, however: By tapping into the network effect a marketer can gain far more value than cost. That's because while cost is still a constant, value grows exponentially based on the number of people who the 'viral' touches (that is assuming it is spread-worthy).
[Deep breath.] Okay, that was way more math than I have thought about in ages and now my head hurts. But I think I had to go through it. I don't think anything I said in the last paragraph is particularly revolutionary, it's more just putting some structure around things lots of people have talked about/noticed. What is more interesting to me about this whole thing is the idea that if you lower the cost, you actually lower the 'critical mass crossover'. Basically, 'going viral' is not an absolute, rather it's based on the cost of production. If you make something for $5 than the 'critical mass crossover' is far lower than spending $500,000. This is possible because all power laws are scale-free, meaning no matter where you look at them they're exponential growth.
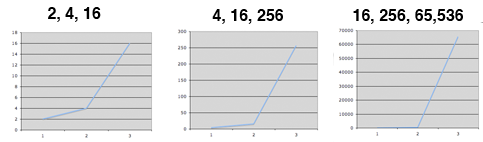
The way I've been explaining scale-free to people lately is with exponents. 22 = 4 and 42 = 16 and 162 = 256. When you look at those four numbers (2, 4, 16, 256) you think that exponential growth kicks in when you square 16, I mean the jump between 16 and 256 is huge. However, if you just isolate 2, 4 and 16, the jump between 4 and 16 is also huge. Below I've put a few charts, while each jump is more radical than the one before it, they are all radical in their own right.
Okay, one more point to make and then I'll leave you alone. If rather than approaching 'viral marketing' with one message, companies tried a number of different, low-cost options, then they might find more success. Each would have a lower 'critical mass crossover' point and you'd only need one success to pay for the rest.
Of course all this assumes a marketer has made something people actually want to pass around, which in and of itself is a lot to ask . . . (For more thinking on this topic I suggest this paper on Big Seed Marketing by Duncan Watts [PDF])