Metcalfe's Plateau
At this point most of us in the geek contingent have heard of Metcalfe's Law. For those that haven't, Metcalfe describes the law named after him like this: "The network effect says that the value of that Ethernet card to the person on whose desk it sits is proportional to the number, N, of other computer users he can connect to. Now multiply this value by the number of users, and you have a value for the whole operation that is roughly proportional to N2." Or as I explained just over a year ago, "If one person has a fax machine it's got no value, if two people have it, it's still got very little value. From there, however, the value really starts to grow for everyone involved and eventually it hits a 'tipping point' where you can't not have one."
It looks like this (taken from Forbes):
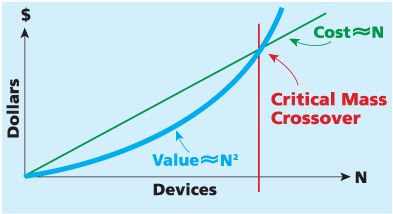
The reason most geeks have heard/talked about Metcalfe's Law is because it's become the de facto religion of Web 2.0: A technological revolution that relies on the network effects described by Metcalfe over 25 years ago. Facebook is the simplest illustration of this, after all a social network without any of your friends is hardly worth joining. Even if Joe Corporate could have gotten on the site when it was just filled with students from 11 universities it would have been pretty boring, after all in a closed system like Facebook, just browsing isn't really an option. Looking at Facebook today, however, you find a site where it's harder to find someone you know who's not on it than who is (especially as someone who had heard of Facebook while they were still in college).
Putting it in context of Metcalfe's Law, it all seems logical. The more people on the network, the greater value the network has, which only attracts more people to the network. I've said it before, and I'll say it again: The number one feature of Facebook is the Facebook network. It's not apps or news feed, it's that every single person you know is on Facebook.
But that can be a bit of a gift and a curse. After all we've all spent a bit of time Facebook gardening: Pulling out the weeds, deleting random friend requests and desperately trying to avoid those stupid vampire bites. At some point, probably around the time Facebook apps launched, I realized that I was actually spending more time gardening than I was doing things I found useful/enjoyable on the site. For the occasional acquaintance I reconnected with, I was approving five friends I either didn't care about talking to or already had other, preferred, modes of communication. Facebook became a bit of a drag.
That's when it occurred to me that I was witnessing Metcalfe's Plateau, a place where the value of the network no longer increases with each additional node. In fact, thanks to spam (as deemed by me), the value of the network had started to decline, I was looking for other places to spend my time online.
I've been noodling on this idea for a while and been trying to figure out just what to say. I don't think it's a particularly new problem. Anyone who's "discovered" a new bar can attest to the initial rise, as you tell all your friends and they tell their friends, which inevitably ends with a place that's so full of random folks that everything you loved about it is gone. In the world of email we see Metcalfe's Plateau even more clearly: Spam. When the network hit a point large enough that you couldn't afford not to have an email, it also hit a point where you could afford to reach massive amounts of individuals for little to no money. Thanks to spam filters, we're able to hold back the flood waters. However, I think it's pretty safe to say for me that new additions to the network are unlikely to provide any additional value to me, since everyone I know or likely will ever know (minus those not born yet or too young to have an email) already has an email. Therefore each new email address (node) holds a certain likelihood to be spam or at least some unrequested contact. (I am not entirely sure about what I'm saying there, it's just a theory now. Feel free to tear it apart.)
As Jeffrey Stibel wrote in a piece called Networks Don't Grow Forever (which inspired me to finally get these thoughts down), "Networks do not always grow more powerful with size and scale. To be sure, Metcalfe’s Law applies to networks up to a point, call it a growth phase. But let us stake our claim to a new Law: all networks eventually hit a point of diminishing returns."
Thinking about it further, I think the distinction probably lies in who reaps the benefits of the network. In other words, the value of the Facebook network to Facebook likely does increase exponentially with each new user, as it allows them to attract even more people to the site. However, for the individual users like us, that value isn't necessarily passed. As Clay Shirky wrote in A Group Is Its Own Worst Enemy,
You have to find a way to spare the group from scale. Scale alone kills conversations, because conversations require dense two-way conversations. In conversational contexts, Metcalfe's law is a drag. The fact that the amount of two-way connections you have to support goes up with the square of the users means that the density of conversation falls off very fast as the system scales even a little bit. You have to have some way to let users hang onto the less is more pattern, in order to keep associated with one another.
Or, as Paul Saffo was quoted as saying in the Economist, "The value of a social network is defined not only by who's on it, but by who's excluded."
As should be obvious at this point, I don't know the answers here. Would love to hear everyone's thoughts. I'm also exploring some of this stuff with a mathematician friend of mine because I'm curious to see whether this idea can be worked out with numbers (and goodness knows I can't figure it out myself).